
This rule for velocity addition is identified as Galilean, and is correct in the limit of small velocities. Most of our experience suggests that velocities should add like ordinary vectors for example, a person walking toward the front of a moving train would, as viewed by a stationary observer, have a net velocity equal to the sum of that of the train and the walker's velocity relative to the train. It has long been accepted that the laws of physics should be covariant, meaning that they should have forms that are (1) independent of the origin of the coordinates used to describe them (leading from an isolated system to the law of conservation of linear momentum) (2) independent of the orientation of our coordinates (leading to a conservation law for angular momentum) and (3) independent of the zero from which time is measured.

Harris, in Mathematical Methods for Physicists (Seventh Edition), 2013 17.8 Lorentz Group In general, for diffraction through a circular aperture in a rigid screen, However, the principle applies at all frequencies. For clarity, the diagram portrays the scattering of a sound wave at some very high frequency where there is minimal diffraction. This is illustrated in Fig. 13.37a, b, and c.
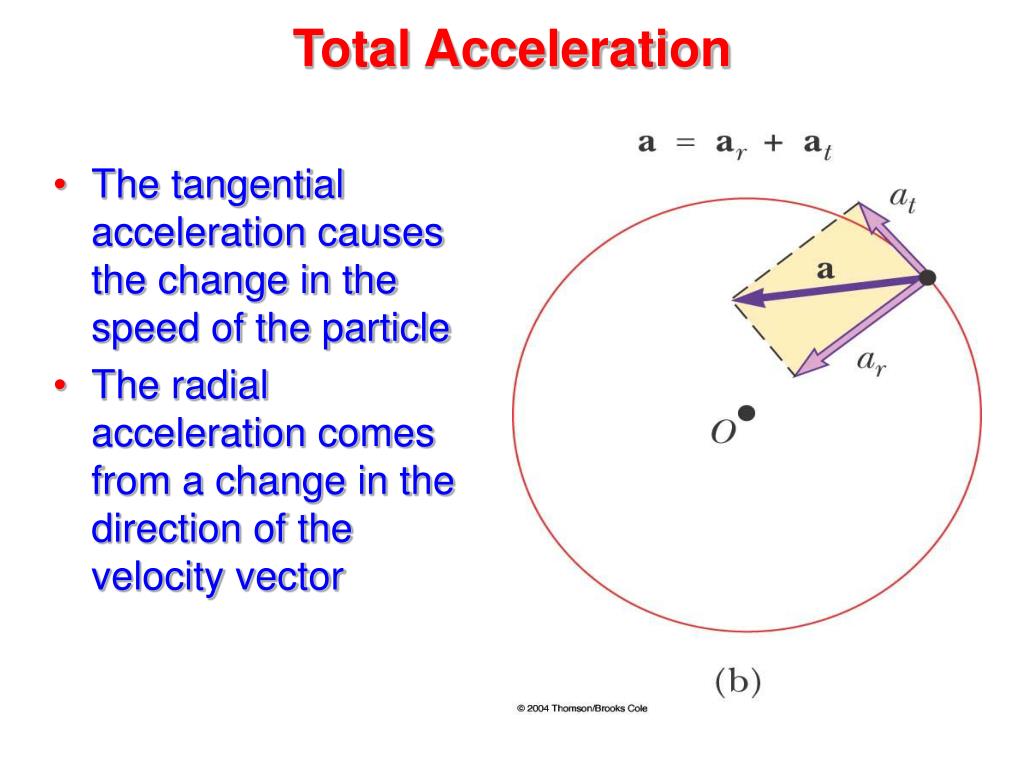
#Direction of acceleration vector 2d plus#
In order to calculate the resultant field on both sides of the screen, we simply add the scattered field to the incident field in the absence of an aperture, i.e., the incident plane wave plus its reflection from a continuous infinite rigid screen plus the radiation from the resilient disk. 13.9, using the monopole part of the Kirchhoff–Helmholtz boundary integral, and satisfies the boundary condition of zero velocity on the screen. Instead, the aperture is treated as the source whereby the pressure is uniform everywhere within it and the aperture acts as a pressure source, namely a resilient disk in an infinite baffle, which we have already evaluated in Sec. However, whereas the rigid disk itself was treated as the source of the scattered wave, it is not so convenient to treat the infinite rigid screen as such. Hence, the resultant velocity is zero at the screen, which is the scattering obstacle, and the pressure in the aperture is the same as that of the incident wave in the absence of any scattering obstacles.
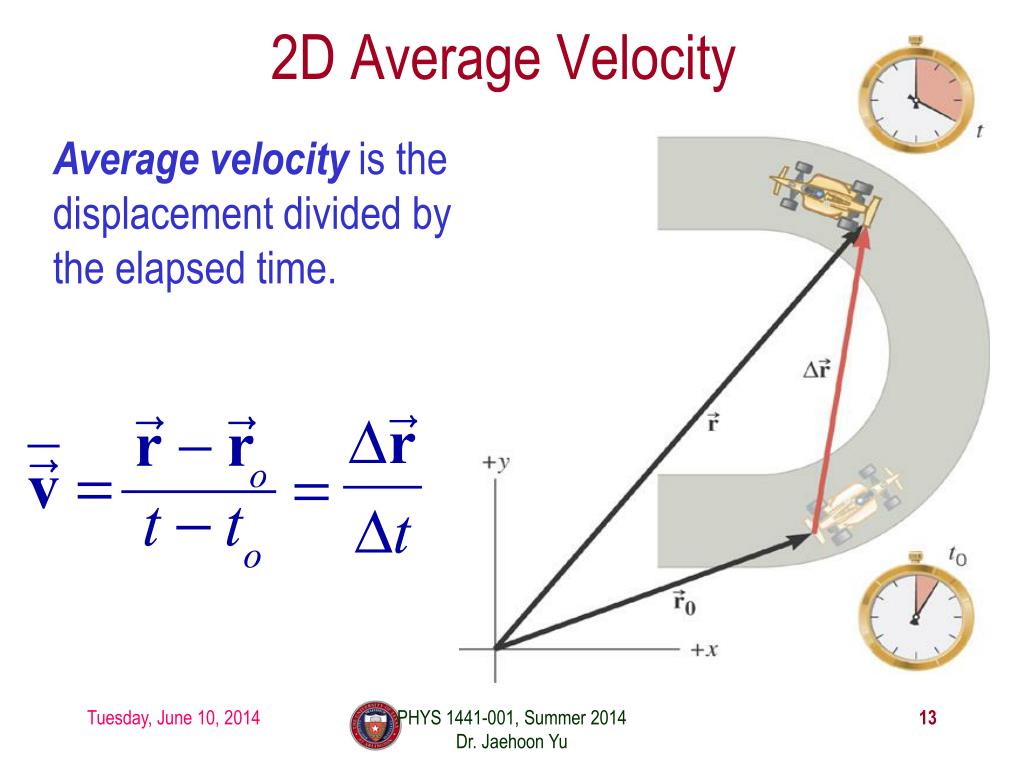
#Direction of acceleration vector 2d free#
Thus, the net acceleration on the object isĮssentially, the boundary conditions for a circular aperture in an infinite rigid screen are the same as those for the complementary rigid disk in free space above and Fig. 13.38d, except that they are interchanged as shown in Fig. 13.37 a. Now, the net force on the object is f = f 1 + f 2. Next, we normalize the direction vectors and to create unit vectors in those directions, obtaining / and /, respectively. The magnitudes of f 1 and f 2 are 10 and 20, respectively. To find the vectors representing f 1 and f 2, we multiply the magnitude of each vector by a unit vector in that vector’s direction. For example, suppose a mass of 5 kg (kilograms) in a three-dimensional coordinate system has two forces acting on it: a force f 1 of 10 newtons 4 in the direction of the vector and a force f 2 of 20 newtons in the direction of the vector. Newton’s Second Law: Newton’s famous Second Law of Motion asserts that the sum, f, of the vector forces on an object is equal to the scalar multiple of the mass m of the object times the vector acceleration a of the object that is, f = m a. The sum of the vector forces on an object is equal to the scalar product of the object's mass and its acceleration vector. The resultant velocity of an object is the sum of its individual vector velocities. ■Īny vector v in ℝ 2 can be expressed as, where θ is the angle v forms with the positive x-axis. The linear combinations of a given set of vectors represent the set of all possible “destinations” that can be reached using those vectors. ■Įvery vector in ℝ n is a linear combination of the standard unit vectors in ℝ n. If the scalar multiple of a vector is the zero vector, then either the scalar is zero or the vector is the zero vector. The commutative, associative, and distributive laws hold for addition of vectors in ℝ n. The sum and difference of two vectors in ℝ 2 can be found using the diagonals of appropriate parallelograms. ■įor any given nonzero vector, there is a unique unit vector in the same direction. Multiplication of a nonzero vector by a nonzero scalar results in a vector that is parallel to the original. The norm (length) of a vector is the distance from its intitial point to its terminal point and is nonnegative. N-vectors are used to represent movement from one point to another in an n-dimensional coordinate system.


 0 kommentar(er)
0 kommentar(er)
